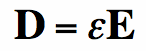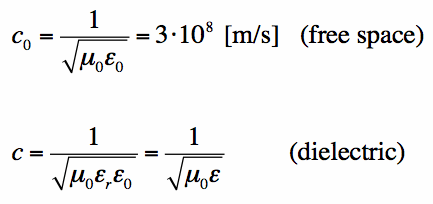Permittivity
Dielectric Constant - Permittivity
In Electromagnetics, permittivity is one of the fundamental material parameters, which
affects the propagation of Electric Fields. Permittivity is typically denoted
by the symbol To understand permittivity, consider Figure 1, in which two charged plates are separated, with equal and opposite charges on either side. Assume for the moment that between the plates, there is no material (vacuum). 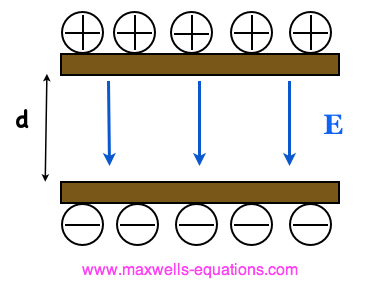 Figure 1. Two Plates with Equal Charge Separated by a Distance d. As you can imagine, there will exist an Electric Field in Figure 1, directed downward (from the positive charge to the negative charge). Now, imagine that some material is placed between the plates. This material is no doubt made up of atoms which often form molecules. And as in the case of water, these molecules often look (electrically) like small dipoles (with a positive charge on one end and negative charge on the other end). This is illustrated in Figure 2 for a water molecule.
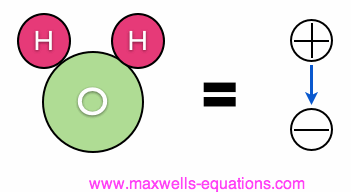 Figure 2. Illustration of an H20 Molecule (water) exhibiting an Electric Dipole Moment. In general, a material will be made up of some lattice or composition of molecules or atoms. These molecules will often have some sort of dipole moment. In the absence of an external electric field, these molecules will align randomly, as shown in Figure 3:  Figure 3. In the absence of an externally applied electric field, the molecules of a material have random orientations. Now, suppose this material is placed between the charged plates of Figure 1. The result is that the molecules will align themselves as shown in Figure 4: 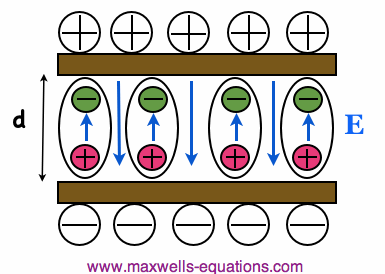 Figure 4. The Molecules are aligned by their Dipole Moment and the external Electric Field. As you can see, the molecules are aligned by their dipole moment and the external electric field. The picture shows something very important - the electric field due to the dipole moment of the materials molecules opposes the external electric field E in Figure 4. The result is that the net electric field is reduced within the material. Generally, permittivity will vary with frequency, temperature, and humidity. For many common materials this variation will be negligible. The permittivity is a measure of how much the molecules oppose the external E-field. If you recall the E-field due to a single point charge of value q [C] at a distance R:
In Equation [1],
In Equation [2], we have added a term
The dielectric constant The permittivity of common materials is given in Table 1.
Properties of the Permittivity in Relation to Maxwell's EquationsThe permittivity is the multiplier that relates the Electric Flux Density and the Electric Field:
In addition, it is known that the speed of light in free space is related to the permittivity and permeability of a medium:
As you can see, the speed of light slows down in a dielectric relative to the speed in a vacuum. Another consequence of this is that the wavelength for an electromagnetic wave of a given frequency is smaller in a dielectric than it is in a vacuum:
Equation [7] is very important to the subject of Antenna Theory. Since antennas often need to be about a half-wavelength long for good radiation, surrounding them in a dielectric can reduce the required size (since the wavelength reduces as well, per [7]).
This page on permittivity or dielectric constant is copyrighted, particularly the application to Maxwell's Equations. Copyright maxwells-equations.com, 2012. All rights reserved. |
.
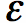is
the permittivity of Free Space, which is measured in Farads/meter. This is the permittivity
of a vacuum (no atoms present). In general, the Electric Field due to a point
charge will be reduced due to the molecules within a material. The effect on
the Electric Field is written in Equation [2]:
.
This term is known as the relative permittivity or dielectric constant. The permittivity
of a medium is expressed as the product of the dielectric constant and the free space permittivity:
