Vector Functions (Vector Fields)
Vector Functions
To understand Maxwell's Equations, we need to understand 3-dimensional vector functions (also known as vector fields). Fortunately, these aren't too complicated. Vector functions are basically 3 stacked functions - the first describes the x-component of the vector, the second describes the y-component and the 3rd function describes the z-component of the vector. Equation 1 gives an example of a vector function (these type of functions are written in bold), and we'll call it A:
The vector function A is a function of 3-spatial variables: (x,y,z). These are just the coordinates
of a 3-dimensional standard Cartesian space. We can write the vector A in terms of 3 non-vector ("scalar") functions,
In Equation [2], Vector functions are relatively simple to evaluate. For instance, if you want to know what the value of A is at location (1,2,3) - you simply substitute this in and evaluate:
Equation [3] states that For Maxwell's Equations, we will only need 3-dimensional vectors (vector functions with x-, y- and z- components). To make things slightly more complicated, we will usually have a time coordinate - but it will still be a 3-dimensional vector function. As an example, look at the vector function B in Equation 4:
The vector function B still only has 3 components,
|

 ,
,  and
and  .
.
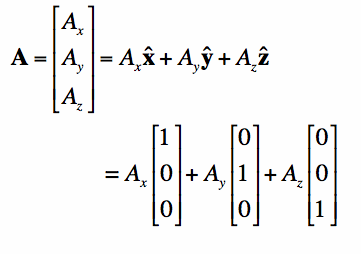
 is a unit vector (a vector with magnitude equal to 1) in the x-direction,
is a unit vector (a vector with magnitude equal to 1) in the x-direction,
 is a unit vector in the y-direction, and
is a unit vector in the y-direction, and  is a unit vector in the z-direction.
is a unit vector in the z-direction.


 ,
,  and
and  . However,
we've added a variable t, which is simply the time component. Now, the vector function B varies with position (x,y,z)
and time (t). To make it clear, if we want to evaluate B at (x,y,z,t)=(1,2,3,4), it is still simple:
. However,
we've added a variable t, which is simply the time component. Now, the vector function B varies with position (x,y,z)
and time (t). To make it clear, if we want to evaluate B at (x,y,z,t)=(1,2,3,4), it is still simple:
