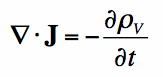The Continuity Equation

The Continuity Equation If we do some simple mathematical tricks to Maxwell's Equations, we can derive some new equations. On this page, we'll look at the continuity equation, which can be derived from Gauss' Law and Ampere's Law. To start, I'll write out a vector identity that is always true, which states that the divergence of the curl of any vector field is always zero: [Equation 1] If we apply the divergence to both sides of Ampere's Law, then we obtain: [Equation 2] If we apply Gauss' Law to rewrite the divergence of the Electric Flux Density (D), we have derived the continuity equation: [Equation 3] Equation [3] looks nice, but what does it mean? The left side of the equation is the divergence of the Electric Current Density (J). This is a measure of whether current is flowing into a volume (i.e. the divergence of J is positive if more current leaves the volume than enters). Recall that current is the flow of electric charge. So if the divergence of J is positive, then more charge is exiting than entering the specified volume. If charge is exiting, then the amount of charge within the volume must be decreasing. This is exactly what the right side is a measure of - how much electric charge is accumulating or leaving in a volume. Hence, the continuity equation is about continuity - if there is a net electric current is flowing out of a region, then the charge in that region must be decreasing. If there is more electric current flowing into a given volume than exiting, than the amount of electric charge must be increasing. And this is exactly what the continuity equation is saying, albeit in complicated mathematical notation. Maxwell's Equations This page on the continuity equation is copyrighted, particularly the derivation from Maxwells Equations. Copyright www.maxwells-equations.com, 2012.