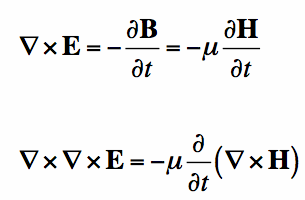The Wave Equation

The Wave Equation One of the most fundamental equations to all of Electromagnetics is the wave equation, which shows that all waves travel at a single speed - the speed of light. On this page we'll derive it from Ampere's and Faraday's Law. We assume we are in a source free region - so no charges or currents are flowing. We want to determine how Electric and Magnetic Fields propagate through the region. To start, let me throw out a vector identity, which is basically a mathematical manipulation that is true for all vector fields: [Equation 1] The left side of Equation 1 is simply the curl of the curl of a vector field. On the right side, I can define the terms for you in the next couple of equations. The first term on the right side of Equation [1] is known as the "gradient of the divergence". However, since we know the divergence of the fields in question will be zero because we are in a source free region. Hence, this term is zero: [Equation 2] The second term on the right side of Equation [1] is known as the Laplacian. This is basically the sum of second-order partial derivatives, as seen in Equation [3]: [Equation 3] OK, so now we can rewrite Equation [1] as: [Equation 4] I've written Equation [4] out as two equations to show that this is true for both the Electric and Magnetic Fields, in source free regions. If we start now with Farday's Law, and take the curl of both sides, we get: [Equation 5] We can rewrite the left side of equation [5] (the curl of the curl of E) with the help of Equation [4]. And we can rewrite the right side of Equation [5] by substituting in Ampere's law: [Equation 6] Equation [6] is known as the Wave Equation It is actually 3 equations, since we have an x-, y- and z- component for the E field. To break down and understand Equation [6], let's imagine we have an E-field that exists in source-free region. Suppose we only have an E-field that is polarized in the x-direction, which means that Ey=Ez=0 (the y- and z- components of the E-field are zero). Further, let's assume that the field is travelling in the z-direction, and there is no variation in the x- and y-directions (this means the partial derivatives with respect to x- and y- are zero). Then Equation [6] simplifies to: [Equation 7] The differential equation in Equation [7] actually has a very nice solution. It turns out any function that can be written as f(z-ct) or f(z+ct) will satisfy the differential equation [7]. This follows from the "chain rule" in calculus: [Equation 8] Equation [8] represents a profound derivation. First, it says that any function of the form f(z-ct) satisfies the wave equation. This means that Maxwell's Equations will allow waves of any shape to propagate through the universe! This allows the world to function: heat from the sun can travel to the earth in any form, and humans can send any type of signal via radio waves they want. Second, a function of the form f(z-ct) represents a wave travelling in the +z direction at a speed of c. From Equation [8], we see this satisfies the wave equation for only one speed - and this is exactly the speed of light: [Equation 9] Maxwell's Equations has just told us something amazing. Electric and Magnetic Fields in "Free Space" - a region without charges or currents like air - can travel with any shape, and will propagate at a single speed - c. This is an amazing discovery, and one of the nicest properties that the universe could have given us. It is pretty cool. Maxwell's Equations This page on the wave equation is copyrighted, particularly the derivation from Maxwells Equations. Copyright www.maxwells-equations.com, 2012.