The Electric Field

The Electric Field Maxwell's Equations is the study of electromagnetics - Electric Fields and Magnetic Fields. Here we talk about the Electric Field - which arises due to electric charges that can be positive or negative. Much of this page is used from out friends at Antenna-Theory.com. Electric Charge and Forces Electric charge exists. It is measured in Coulombs. Atoms consist of electrons (negatively charged), neutrons (no charge) and protons (positively charged). But charge can also exist on metals, in clouds (which gives rise to lightning) and on doorknobs (which gives you a shock every now and then). If electric charge is moving, then this flow of electric charge is known as electric current. Further, objects with an electric charge exhibit a force on each other. Opposite charges attract, and like charges repel each other, as shown in Figure 1. 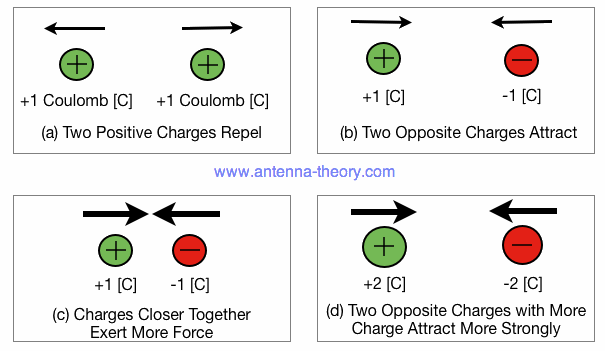Figure 1. Electrically Charged Particles Repel or Attract Each Other. The force depends on a few things: the magnitude of each charge (measured in Coulombs) and the distance between the charges (R). The force equation is for two charges is given by: [Equation 1] In Equation [1], the force is measured in Newtons [N]. The charges are of magnitude q_1 and q_2. If both charges have the same sign (both positive or both negative) the force felt by each charge is directed away from the opposite charge. If they are opposite in sign, the forces pushes the charges together. The term is known as the permittivity of free space and is a fundamental physical constant of our universe. The Electric Field The previous discussion dealt with the interaction of two charged particles at a distance. But how do the particles know about each other? If we imagine an isolated charge at some location X, does it have an effect away from this location? The answer is yes. The charge is surrounded by an Electric Field everywhere in space. The Electric Field (or E-field) at any location X is defined as the force a charge of +1-Coulomb would experience if it was placed at location X. This is written as "the E-field is the force per unit charge". So, the E-field from a point charge (Equation [1]) can be found by setting q_2 equal to +1. Then we have the E-field due to a point charge of value q Coulombs: [Equation 2] Equation [2] gives the magnitude of the Electric Field. The Electric Field is a vector quantity - it has a magnitude and direction. For positive charges (q>0) the E-field points away from the charge, and for negative charges the E-field points towards the charge. The E-field in Maxwell's Equations is always a 3-dimension vector field. This means it has 3 components - an x-, y- and z-component that define the Electric Field in the x-, y- and z-directions. Figure 2 shows the Electric Field surrounded isolated point charges. Note the direction of the E-field lines, and also that the magnitude of the Electric Field decreases with distance from the charge (R gets larger as you move away from the charge). 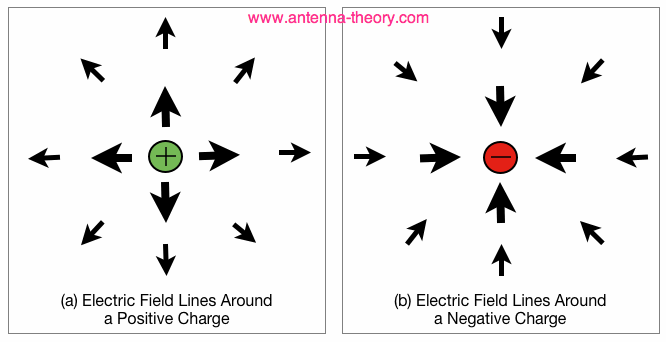Figure 2. Electrically Charged Particles Repel or Attract Each Other. The Electric Field has units (dimensions) of Newtons/Coulomb [N/C], which is equivalent to Volts/meter [V/m]. In general, the Electric Field obeys the super-position principle: the total Electric Field from a number of charges is equal to the sum of the electric fields from each charge individually. Since the E-field is a vector, vector addition applies. Maxwell's Equations The Electric Field page is copyrighted, and belongs to Maxwells-Equations.com. Copyright Maxwells-Equations.com, 2012.