Permeability
Permeability
The
permittivity of a material relates the
Electric Flux Density to the
Electric Field. Similarly, materials can be classified by
their permeability, which relates the
Magnetic Flux Density to the
Magnetic Field, via Equation [1].
The permeability is most often denoted by the greek symbol mu (
The permeability is measured in units of Henries/meter [H/m], which has dimensions of inductance per unit length. Just as permittivity is associated with the alignment of bound molecules electric dipole moments, the permeability relates to the orientation of bound magnetic particles within a material. In a simple sense, the permeability is a meaure of how easily a magnetic field can pass through a medium.
The permeability of a vacuum is denoted by
The permeability of a medium (
The relative permeability of a medium can actually be less than 1. This is known as Diamagnetism. When this happens, the material actually creates an internal magnetic field in opposite to the externally applied magnetic field. A medium (material) with a relative permeability greater than 1 is known as paramagnetic. In these materials, the B and H fields are linearly related per Equation [1], and the intensity (magnitude) of the magnetic field does not alter the value of the permeability.
In contrast, Ferromagnetism in materials exhibit hysteresis. In this manner,
the permeability is a function of the strenght of the applied fields and the history
(the applied magnetic field versus time) of the applied field. These materials
often have very high values for The permeability of common materials is given in Table 1.
The permeability page is copyrighted, particularly the application to Maxwell's Equations. Copyright maxwells-equations.com, 2012. All rights reserved. |
).
,
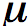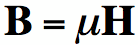
and is equal to:
, which is
a measure of the permeability of a medium relative to that of a vacuum:
