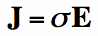Conductivity
Conductivity
On this page, we define electrical conductivity. Conductivity is a measure of how easily electric current can flow through a given material. That is, for a given Electric Field in a material, a higher conductivity material will produce more current flow than a low conductivity material. If you understand electric circuits, then conductivity is analogous to the inverse of resistance. The electric field is similar to voltage, so voltage across a small resistor (high conductivity) will produce a large amount of current. Voltage across a large resistor (low conductivity) will produce a smaller amount of electric current.
Conductivity represents power loss within a material. A material is known
as "lossless" if the conductivity is zero (
When the conductivity is not zero, then an Electric Field flowing through the material
will induce an
Electric Current Density (J). The relationship
between E, J, and
Some materials, such as copper or steel (or metals in general) have very high conductivities, and the conductivity can often be approximated as infinite. This means the material has a resistance of zero. For these materials, we can see from Equation [1] that the Electric Field must zero within these materials. If it was not zero, then from Equation [1] the current density would be infinite, which is not the case. Hence, while we can have current flow through metals or high conductivity materials, the Electric Field inside these materials must be zero. In textbooks, these materials are often referred to as PEC (perfect electric conductors), so that the conduction loss can be ignored.
Consider now materials with a conductivity greater than zero, but also non-metallic materials so that the conductivity is not extremely high. In this case, we may have electric current flowing in a material, along with an associated Electric Field. When electric current flows through a material, some of the energy is converted to heat (the energy is then lost from the Electromagnetic Wave or current). Materials with with medium-range conductivities are known as lossy materials. An example of a lossy material with a mid-range value for conductivity is Carbon. [In fact, Carbon is used inside materials for absorbing electromagnetic waves in antenna measurements inside a chamber known as an anechoic chamber.] Generally, we can divide materials into 3 regions by their conductivity, as shown below:
 Figure 1. Classifying Materials By Their Conductivity. Electrical Conductivity is measured in units of Siemens/meter [S/m]. Siemens is the inverse of Ohms, or resistivity. For this reason, sometimes people refer to Siemens as Mhos (ohms spelled backwards). The electrical conductivity of common materials is given in Table 1.
The conductivity page is copyrighted, particularly the application to Maxwell's Equations. Copyright maxwells-equations.com, 2012. All rights reserved. |
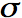=0).
Materials like air and vacuum (space) have no conductivity.
